Day 19: In-class Assignment: Modeling forest fires with an Agent-based Model (Part II)#
✅ Put your name here.
#✅ Put your group member names here.
#
Goals of this assignment#
The primary goal of this assignment is to model the spread of a forest fire using an agent-based model (ABM). In doing so, we will:
Use ABM to model forest fires
Examine and quantify the concept of a “tipping point” in a model.
Assignment instructions#
Work with your group to complete this assignment. Upload the assignment to D2L at the end of class.
Welcome to Part 2 of the forest fires ICA!#
We have split this assignment over two days, so that you can become more comfortable with material. Last class, we built the basics of the forest fire model. Today, we are going to put all these pieces together to complete the model and analyze the tipping point! Let’s get started!
Below, we show the rules again. We’ll incorporate all of the code that you worked on last class. It may look a little different than the code that you and your group developed. If you want to bring over some of your code from Part 1, feel free to do so!
Redefining the Rules for Our Model#
Setup#
The model is a two-dimensional square \(N \times N\) array that represents the forested region we’re simulating. The cells in the array can have three values:
0 (empty)
1 (trees)
2 (on fire)
At the beginning of the model, a user-specified fraction of the cells \(f_\text{trees\_start}\) are randomly filled with trees and the remaining cells are empty.
One edge of the board (say, the entire leftmost column) is set on fire.
Neighborhoods#
Each cell has a “neighborhood” that is composed of its four neighbors to the left, right, above, and below it. If a cell is along one of the edges of the array, only consider the neighbors that it has (i.e., don’t try to go out of the bounds of the array).

Evolving with Time#
The model takes steps forward in time, where every cell is modified based on the previous step. The model evolves as follows:
If the cell was empty last turn, it stays empty this turn.
If the cell is a tree and any of its neighbors were on fire last turn, it catches on fire.
If the cell was on fire last turn, the fire has consumed all of the trees and it is now empty.
Ending Conditions#
The model evolves forward in time until all of the fires have burned out.
After this happens, you can calculate the fraction of the cells that still have trees at the end of the model (\(f_\text{trees\_end}\)) and the fraction of cells that are empty (\(f_\text{empty}\)). The fraction of burned cells, \(f_\text{burned}\), is just the difference between the fraction of cells that were initially trees and the fraction of cells that are trees at the end of the model; in other words,
\(f_\text{burned} = f_\text{trees\_start} - f_\text{trees\_end}\)
Your mission:#
Your mission is to answer the question: “How does the spread of fire relate to the density of the forest?”
More precisely, we’re asking “How does \(f_\text{burned}\) depend on \(f_\text{trees\_start}\)?”
Functions from Last Class#
Last class, we built a function that plots the array, a function that initializes the board, and a function that advances the board based on a set of rules.
Make sure to execute the following cells before you move on!
Importing Libraries#
# standard includes
import numpy as np
import numpy.random as rand
%matplotlib inline
import matplotlib.pyplot as plt
# Next we are going to import some specific libraries we will use to get the animation to work cleanly
from IPython.display import display, clear_output
import time
Plotting the Board#
The plot_grid function takes in a given array, finds the positions on the board that are a tree or fire, and displays them as such.
def plotgrid(myarray):
# First create two vectors based on the x and y sizes of the grid
x_range = np.linspace(0, myarray.shape[1]-1, myarray.shape[1])
y_range = np.linspace(0, myarray.shape[0]-1, myarray.shape[0])
# Use the numpy meshgrid function to create two matrices
# of the same size as myarray with x and y indexes
x_indices, y_indices = np.meshgrid(x_range, y_range)
# Make a list of all the x and y indexes that are either trees or fire.
tree_x = x_indices[myarray == 1];
tree_y = y_indices[myarray == 1];
fire_x = x_indices[myarray == 2];
fire_y = y_indices[myarray == 2];
# Plot the trees and fire.
plt.plot(tree_x, myarray.shape[0] - tree_y - 1, 'gs',markersize=10)
plt.plot(fire_x, myarray.shape[0] - fire_y - 1, 'rs',markersize=10)
# Set the x and y limits so we don't cut off the shapes
plt.xlim([-1,myarray.shape[1]])
plt.ylim([-1,myarray.shape[0]])
# Removing tick marks
plt.tick_params(axis='both', which='both',
bottom=False, top=False, left=False, right=False,
labelbottom=False, labelleft=False)
Initializing the Forest#
The set_board function creates the initial state of the board based on the provided density, setting the leftmost edge as ‘on fire.’
def set_board(board_size=50,f_trees_start=0.5):
'''
Creates the initial game board.
Inputs:
board_size: length of one edge of the board
f_trees_start: probability that a given cell is a tree
(effectively the tree density)
Outputs a 2D numpy array with values set to either 0, 1, or 2
(empty, tree, or fire)
'''
# all cells initialized to 'empty' (0) by default
game_board = np.zeros((board_size,board_size),dtype='int64')
# loop over board and roll the dice; if the random number is less
# than f_trees_start, make it a tree.
for i in range(board_size):
for j in range(board_size):
if rand.random() <= f_trees_start:
game_board[i,j] = 1
# set the whole left edge of the board on fire. We're arsonists!
game_board[:,0] = 2
return game_board
Evolving the Board#
The advance_board function:
Takes in the current board,
Defines a new board with the same properties as the old board but full of 0s to start, and then
Returns that new board where the positions of the trees and fire have been updated.
Based on these rules:
Each cell has a “neighborhood” that is composed of its four neighbors to the left, right, above, and below it. (Note: not the diagonal elements!) If a cell is along one of the edges of the array, only consider the neighbors that it has, and doesn’t try to go out of the bounds of the array!
The model takes steps forward in time, where every cell is modified based on the previous step. The model evolves as follows:
If the cell was empty last turn, it stays empty this turn.
If the cell is a tree and any of its neighbors were on fire last turn, it catches on fire.
If the cell was on fire last turn, the fire has consumed all of the trees and it is now empty.
def onBoard(i,j,image):
if i <= image.shape[0]-1 and i >= 0 and j <= image.shape[1]-1 and j >= 0:
return True
else:
return False
def getNeighborValues(i,j, board):
neighborhood = [(i-1, j), (i, j-1), (i+1, j), (i, j+1)]
neighbor_values = []
for neighbor in neighborhood:
if onBoard(neighbor[0], neighbor[1], board):
neighbor_values.append(board[neighbor[0], neighbor[1]])
return neighbor_values
def advance_board(game_board):
'''
Advances the game board using the given rules.
Input: the initial game board.
Output: the advanced game board
'''
# create a new array that's just like the original one, but initially
# set to all zeros (i.e., totally empty)
new_board = np.zeros_like(game_board)
# loop over each cell in the board and decide what to do.
for i in range(game_board.shape[0]):
for j in range(game_board.shape[1]):
# if the cell was empty last turn, it's still empty.
# if it was on fire last turn, it's now empty.
if game_board[i,j] == 0 or game_board[i,j] == 2:
new_board[i,j] = 0
# now, if it's a tree we have to decide what to do.
if game_board[i,j] == 1:
# initially make it a tree
new_board[i,j] = 1
# If one of the neighboring cells was on fire last turn,
# this cell is now on fire!
if 2 in getNeighborValues(i,j,game_board):
new_board[i,j] = 2
# return the new board
return new_board
Reviewing the Code#
✅ Compare each of the functions given above to the code you wrote last class, particularly the advance_board function. In the cell below, write down any changes you notice. Which version of the functions makes more sense to you?
✎ Put your answer here
Part 4: Analyzing the state of the board#
Now, that we have loaded in all our functions from last class, we have one more step before seeing our complete forest fire model.
As we run our model, we want to know what fraction of the board is empty and what fraction is covered with trees. You need to add code to compute these values. A bit of skeleton code is provided for you to help guide your coding efforts.
✅ 4.1 Finish the code below so that it calculates the statistics of the board.#
def calc_stats(game_board):
'''
Calculates the fraction of cells on the game board that are
a tree or are empty.
Input: a game board
Output: fraction that's empty, fraction that's covered in trees.
'''
# use numpy to count up the number that are empty and calculate the fraction
frac_empty =
# do the same for trees
frac_tree =
# return it!
return frac_empty, frac_tree
4.2 Putting it all together!#
The following code takes all of the above functions and puts them in order along with some animation code so that you can see your fire spread. If your functions above were written correctly, this could should just work.
In the code below, we are calling our advance board function at each step.
Part 5: The tipping point#
What is a “tipping point”?#
This model also demonstrates the concept of a “critical threshold” or a “tipping point”. This is a phenomenon that occurs when a small change in an input parameter results in a large change in outcome. This is a phenomenon that shows up in both simple and complex models and happens in such varied circumstances as forest fires, the spread of disease in populations, and the transfer of information within a population.
Finding the “tipping point”#
In order to find the tipping point, i.e. the point at which the fire spreads much more substantially, we want to loop over many values of \(f_\text{trees\_start}\) (say, values from 0.01 to 1.0, in steps of 0.01) and run the model many times. If we keep track of the fraction of cells that are burned for each starting condition, we can show how \(f_\text{burned}\) and \(f_\text{trees\_start}\) relate to each other.
The fraction of burned cells, \(f_\text{burned}\), is just the difference between the fraction of cells that were initially trees and the fraction of cells that are trees at the end of the model; in other words,
\(f_\text{burned} = f_\text{trees\_start} - f_\text{trees\_end}\)
Your plot should look something like this:
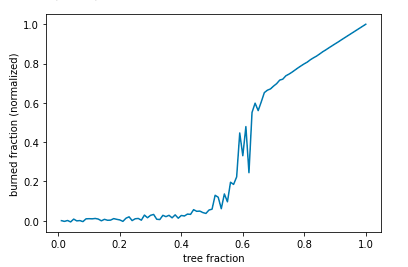
✅ 5.1 The code below is incomplete, fill in the “___” spots with code to make a plot to observe where the tipping point occurs.
board_size = 50
f_tree = []
f_burned = []
# Complete this line
for tree_fraction in ____
# Complete this line
game_board = ____
on_fire = True
while on_fire == True:
# Complete this line
game_board = ____
# Complete this line
frac_empty, frac_trees = ____
if frac_empty + frac_trees == 1.0:
# Complete this line
on_fire = ____
# Complete this line
f_tree.append(____)
f_burned.append(frac_empty - (1.0-tree_fraction))
plt.plot(f_tree, f_burned)
plt.xlabel("tree fraction")
plt.ylabel("burned fraction (normalized)")
✅ Follow up task:#
Describe the model’s behavior. Do you observe a “tipping point” in \(f_\text{burned}\)? That is, is there an abrupt change in behavior in \(f_\text{burned}\) as you increase \(f_\text{trees\_start}\)? Does it agree with what you saw when you were experimenting with the NetLogo model?
✎ Put your answer here
✅ Follow up task:#
Now that you have completed the forest fire model, how would you describe the process to someone who has did not complete this activity? What steps are required to set up the model? How does the forest fire move? What did you learn about the tipping point?
Make sure to also chat about this with an instructor about this.
✎ Put your answer here
Part 6: Exploring new initial conditions#
So far, we have been setting up fire from the left edge of the forest. Now, we are going to observe how the model changes if we start the fire in a different place.
For example, set the fire in a single square in the middle of the forest and examine the tipping point. Does this change where the tipping point occurs? Copy and modify the code and also put down your observations in a Markdown cell below.
Repeat this analysis for multiple other starting points for the fire. Get creative! Have fun!
✎ Put your analysis here
Time Permitting#
If you have time left in class, brainstorm with your group (and Google) what agent-based models may be good for (other than forest fires). For those examples, discuss what aspects would be similar to the forest fire and what would be different. What would your initial conditions look like? How would you expect the model to run? What initial thoughts do you have about the tipping point?
Discuss with your group and write down your thoughts in a Markdown cell below.
✎ Put your answer here
Congratulations, you’re done!#
Submit this assignment by uploading your notebook and the pictures of your model planning session to the course Desire2Learn web page. Go to the “In-Class Assignments” folder, find the appropriate submission link, and upload everything there. Make sure your name is on it!
© Copyright 2023, Department of Computational Mathematics, Science and Engineering at Michigan State University

✅ Comment the code to indicate that you know what its doing!#
✅ Task: Run the model for a few values of \(f_\text{trees\_start}\); say, 0.25, 0.5, 0.75, and 1.0. Do you notice any differences in the behavior of the model as you change \(f_\text{trees\_start}\)? Put down your answer in the cell below.
✎ Put your answer here