Day 16 Pre-class Assignment: Introduction to Modeling with Ordinary Differential Equations

✅ Put your name here.

Goals for Today’s Pre-Class Assignment

In this assignment, you will:

• Learn how to model changing systems mathematically

• Qualitatively describe how a system is changing

• Explore using Python to numerically model these systems

Assignment instructions

This assignment will introduce how we can model real-world examples with ordinary differential equations and how we can use Python to solve them numerically.

This assignment is due by 11:59 p.m. the day before class, and should be uploaded into the appropriate “Pre-class assignments” submission folder. Submission instructions can be found at the end of the notebook.

---

1. What is an Ordinary Differential Equation?

Video

Watch this video on MediaSpace

✅  1.1 Question

In your own words, summarize the purpose of ordinary differential equations (ODEs).

✎ Put your answer here

✅  1.2 Question

What is an example of a model that we have worked with previously in class that could be modeled using an ODE?

✎ Put your answer here

✅  1.3 Question

Let’s say we’re working with some (mathematical) function \(f(t)\) and the differential equation \(\frac{df}{dt}\). What does it mean if you have a large positive derivative? (i.e., \(\frac{df}{dt}\) is a very big positive number.)

✎ Put your answer here

✅  1.4 Question

What does it mean if you have a large negative derivative? (I.e., \(\frac{df}{dt}\) is a very big negative number.)

✎ Put your answer here

---

2. An introduction to solving ODEs numerically with Python

Video

Watch this video on Mediaspace

✅  2.1 Question

What is an update equation? What information is needed for an update equation in order to be able to solve an ODE problem numerically?

✎ Put your answer here

✅  2.2 Question

If we know the value of \(x_1\) at time \(t_1\), and we know the differential equation \(\frac{dx}{dt}\), how could we find the value of \(x_2\) at time \(t_2 = t_1 + \Delta t\)?

✎ Put your answer here

✅  2.3 Question

In your own words, explain how you used the differential equation \(\frac{dx}{dt}\) to find the value \(x_2\) in the previous question.

✎ Put your answer here

✅  2.4 Question

Look at the solution to the differential equation for population growth below with a timestep of 50 years. How might that change with a time step of 10 years? What about 100 years?

✎ Put your answer here

---

3. The Population Growth Model

Recall from the video that the ordinary differential equation describing population is:

\begin{equation} \frac{dP}{dt} = kP\Big(1-\frac{P}{C}\Big), \end{equation}

where \(P =\) population, \(k =\) growth rate, and \(C =\) the carrying capacity. If we make our initial population be 1 billion and vary the other parameters, the solution \(P(t)\) looks like the figures below.

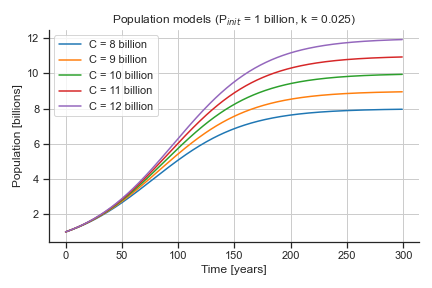
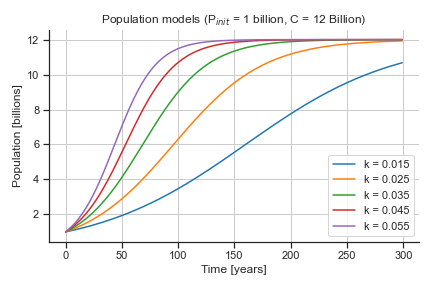
✅  3.1 Question

What are the parameters of our population model? What value (or values) change with time in this model?

✎ Put your answer here

✅  3.2 Question

Look at the figure below showing different values of initial population \(P_0\). How does the population growth change with different initial values?

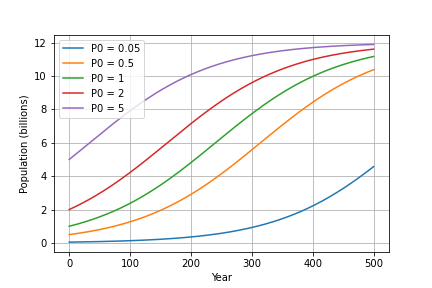
✎ Put your answer here

---

4. Coding the Derivative

To do numerical integration for a model, we need to compute a new value for our solution for each time step using our previous value, the derivative, and the time step. Recall that we refer to these as update equations. To calculate the derivative at each time step for use in the update equations, we will use a function. The function must:

1. take in the current value of the solution as the first argument

2. include any relevant model parameters as additional arguments, and

3. return the value of the derivative.

✅  4.1 Task

In the cell below, fill in the derivs function with the appropriate input arguments, return value, and equation for the derivative of population with respect to time (\(\frac{dP}{dt}\) from Part 3).

# Define a function that computes the derivatives
def derivs(# PUT YOUR INPUT(S) HERE, make sure to include current population value and the model parameters):
    # Define the differential equation for the population model
    
    #return the value of the derivative
    return 

✅  4.2 Task

Now test your derivs function to see if it works by calling it with and initital population value of \(P_0 = 1\) billion and assuming \(k = 0.01\) and \(C=12\) billion. You should get a value of about ~9170000 (or ~0.00917 if you fed in your population and carrying capacity values in units of “billions).

# Put your code here

✅  4.3 Questions

What does the output of the derivs function represent? How could you use the output of the derivs function to calculate population values (I.e., \(P(t)\))?

✎ Put your answer here

✅  4.4 Task

To get the solution for many time steps, we will need to use the derivative in a loop that calculates the values using update equations. In the cell below, write pseudocode that describes the structure of this loop. Be as detailed as you can!

✎ Put your answer here

---

Assignment wrapup

Please fill out the form that appears when you run the code below. You must completely fill this out in order to receive credit for the assignment!

from IPython.display import HTML
HTML(
"""
<iframe 
	src="https://cmse.msu.edu/cmse201-pc-survey" 
	width="800px" 
	height="600px" 
	frameborder="0" 
	marginheight="0" 
	marginwidth="0">
	Loading...
</iframe>
"""
)

Congratulations, you’re done!

Submit this assignment by uploading it to the course Desire2Learn web page. Go to the “Pre-Class Assignments” folder, find the appropriate submission link, and upload it there.

Copyright © 2023, Department of Computational Mathematics, Science and Engineering at Michigan State University, All rights reserved.