Pre-Class Assignment: Further exploration of SVMs

Pre-Class Assignment: Further exploration of SVMs#

Day 21#

CMSE 202#

✅ Put your name here
#

Goals for today’s pre-class assignment#

Observing non-linear separability (sklearn.datasets.make_circles)
Graphing data in 3D
Explaining how a RBF kernel works like a nearest neighbors model

Assignment instructions#

This assignment is due by 11:59 p.m. the day before class and should be uploaded into the appropriate “Pre-class assignments” submission folder in the Desire2Learn website.

Imports:#

# imports for the day
import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm
from sklearn.datasets import make_circles
from mpl_toolkits.mplot3d import Axes3D

1. Nonlinear data#

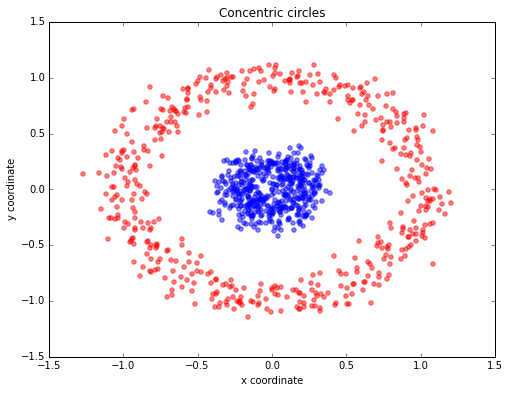
Working with linearly separable data certainly makes life easy, but that is simply not the case many times when we’re working with data. Review data in the figure at the beginning of the assignment. Clearly the data in that plot are not linearly separable. It turns out, we can find a way to make it linearly separable and we will explore this during class.

1.1 `sklearn.datasets.make_circles` data generators#

Sticking with the scikit-learn datasets page and in particuar Section 7.3, we see make_circles which allows us to make data similar to that seen in the figure above.

Using the documentation, create an example data set with two “circles”, a 2-class data set. It should:

have 100 samples
two classes
set the random_state value so that you can generate the same “circles” every time.

# put your answer here

2. Graph the circles#

Did it work? As always, it’s hard to tell if we ended up with what we wanted without visualizing it.

✅ Do This: Graph the result of the make_circles operation. Color all the elements of one class one color and the elements of the other class the other color.

As a reminder:

you can create a list/array with color assignments for each data element based on their class. Your colors can be strings like 'red', integer numbers (that will map to whatever matplotlib cmap you use), or hex code values – it’s up to you.
try playing with the random_state value and see if you can get some “blobs” that are relatively “close” to each other. It should be the case that if you use the same random_state value each time that you get the same distribution of data. Remember, “random” means “relatively random” here. That is, predicting the next value in a sequence should be (statistically speaking) random. However, start with the same seed value (which is what random_state is for this process) you get the exact same sequence.

# put your answer here

3. Adding a dimension to linearly separate the data#

It’s hard to see how we could separate these two classes given their overlap/shape, and that is likely true in the 2D format we are looking at currently. But what if we added a 3rd dimension based on the features of the data that we have? That is, can we use the existing X and Y values to make a new dimension that would that help to linearly separate the data?

As you saw in this video from the previous pre-class assignment, creating these new dimensions from the data is part of what an SVM does. For this assignment, we will try to do this manually.

First, let remind ourselves of 3D plots.

3.1 Making a 3D scatter plot#

To setup a 3D scatter plot, you need the following steps (found in this tutorial; you can see the code if you click on the plot). We can generate some random values and try it out.

x = np.random.randint(-5, 5, 100)
y = np.random.randint(-5, 5, 100)
z = np.random.randint(-5, 5, 100)
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure(figsize = (10, 7))
ax = plt.axes(projection ="3d")
 
# Creating plot
ax.scatter3D(x, y, z, color = "blue")
plt.title("simple 3D scatter plot")

✅ Do This: Plot your circle data in 3D. Because we don’t have a third/\(z\) dimension you can just pass a fixed value for \(z\). In fact, you can just use a single number. As before, mark the two classes in two different colors.

# put your answer here

3.2 Trying to make the data linearly separable#

Let’s try to separate these circles of data using the existing values to compute \(z\)-values that would make it possible to separate the.

✅ Do This: Try to add a third dimension to the data, by calculated \(z\)-values based on the existing values. This is called a “transformation” of the data.

What might be a procedure to do that? You might have to think about this for a moment or perhaps poke around a bit on the internet. Do your best to come up with something that you think should work.

Make a 3D plot of your transformed data.

# put your code here

✅ Question: What transformation did you use to separate the data in the third, \(z\) dimension? Do you feel you were successful in separating the data?

✎ Do this - Erase this and put your answer here.

4. Alternative Kernels for SVM#

The linear kernel is one of a number of possible kernels that an SVM can use. One common choice for dealing with nonlinear data is the Radial Basis Function (RBF) Kernel. The video from the previous class assignment has a bit of information about this kernel.

✅ Do This: Review this section of the video for a conceptual description how the RBF works like a nearest neighbors model. Deeper, more technial details on the RBF are readily available online, but extend a bit beyond the scope of this course at the present time. Feel free to dig into them if you wish!

from IPython.display import YouTubeVideo
from datetime import timedelta
start=int(timedelta(hours=0, minutes=17, seconds=29).total_seconds())
YouTubeVideo("efR1C6CvhmE",width=800,height=450,start=start)

✅ Question: How does a the RBF work like a nearest-neighbors model?

✎ Do this - Erase this and put your answer here.

Follow-up Questions#

Copy and paste the following questions into the appropriate box in the assignment survey include below and answer them there. (Note: You’ll have to fill out the assignment number and go to the “NEXT” section of the survey to paste in these questions.)

When we can’t easily linearly separate classes in our data in its default form, what can we do with the data in order to find a linear decision boundary that can separate the data?
How does the RBF act similarly to the nearest-neighbor algorithm?

Assignment wrap-up#

Please fill out the form that appears when you run the code below. You must completely fill this out in order to receive credit for the assignment!

from IPython.display import HTML
HTML(
"""
<iframe 
	src="https://cmse.msu.edu/cmse202-pc-survey" 
	width="800px" 
	height="600px" 
	frameborder="0" 
	marginheight="0" 
	marginwidth="0">
	Loading...
</iframe>
"""
)

Congratulations, you’re done with your pre-class assignment!#

Now, you just need to submit this assignment by uploading it to the course Desire2Learn web page for today’s submission folder (Don’t forget to add your name in the first cell).