Homework Assignment 2#
Modeling planets’ orbits#
(Notebook 1 of 2)#
✅ Put your name here.
#✅ Put your GitHub username here.
#Table of contents#
Pre Assignment Survey (0 points + 1 git)
Planet orbits and migration (14 points + 1 git)
Modeling planet migration (33 points + 1 git)
Learning Goals#
By the end of this assignment, you should be able to:
Define planet migration types
Compare orbit shapes, based on the mass of the planet/the star, the radius of the orbit, and the eccentricity
Be able to find the orbital period from orbit properties
Be able to write methods and attributes of a class, based on the description of the final needed result
Be able to define agents using classes in Python and interactions between them using methods of Python classes.
Describe an agent-based model that accurately presents the properties of a planetary system.
Implement the evolution of the agent-based model by correctly applying the rules for the model and updating the state of the agents in the model.
Be able to identify needed forces and their effect on modeling planet migration.
Be able to visualize and describe the results of planetary migration simulation.
Work through the following assignment, making sure to follow all of the directions and answer all of the questions.
The assignment is split into two notebooks:
Notebook 1 of 2 is worth 14 + 33 + 3 = 51 points
Notebook 2 of 2 is worth 1+ 42 + 1 = 44 points for a total of 95 points. Point values for each part are included in the section headers and question prompts.
This assignment is due at 11:59 pm on Friday, March 21st. It should be uploaded into the “Homework Assignments” submission folder for Homework #2 on D2L. Submission instructions can be found at the end of the notebook. You must also fill out a survey regarding this assignment. The link to this survey can also be found at the end of the notebook.
Pre-assignment Survey#
Please fill out the pre-assignment survey here.
import numpy as np
import matplotlib.pyplot as plt
🛑 STOP#
Pause to commit your changes to your Git repository! (1 points)
Create a hw-02 folder in your cmse202-s25-turnin repo. Take a moment to save your notebook, add and commit the changes to your Git repository using the commit message “Initial commit of HW 2”, no need to push the changes to GitHub yet, but you can if you want.
Part 1: Planet orbits and migration types (14 Points)#
✅ Do this: Watch these 2 videos and answer the questions below.
from IPython.display import YouTubeVideo
YouTubeVideo('pRvVK2m_wGE', width=800, height=400)
YouTubeVideo('BGPBNeTFXZk', width=800, height=400, end=260)
✅ Question 1.1 (1 point): What shape is Earth’s orbit?
✎ Do This - Erase the contents of this cell and replace it with your answer to the above question! (double-click on this text to edit this cell, and hit shift+enter to save the text)
✅ Question 1.2 (3 points): How many types of orbit shapes did the 1st video mention? Which shape is more common for satellites and planets in our Solar system?
✎ Do This - Erase the contents of this cell and replace it with your answer to the above question! (double-click on this text to edit this cell, and hit shift+enter to save the text)
✅ Question 1.3 (1 point): How many types of migration did the 2nd video mention?
✎ Do This - Erase the contents of this cell and replace it with your answer to the above question! (double-click on this text to edit this cell, and hit shift+enter to save the text)
✅ Question 1.4 (2 points): We see hot Jupiters (planets the size of Jupiter but hot!) in orbits very, very close to their stars. Because of the temperature in these regions, there is no way that planets the size of Jupiter (300 times Earth’s mass and 11 times Earth’s radius) could form because the star would just steal all the gas and not let the planet to form. But we still see hot Jupiters in those orbits. How do they end up near their stars?
✎ Do This - Erase the contents of this cell and replace it with your answer to the above question! (double-click on this text to edit this cell, and hit shift+enter to save the text)
Orbital period#
An important parameter for a planet orbiting a star is its orbital period. This is the time it takes for the planet to travel 1 whole orbit. For example, for the Earth the orbital period is 1 year. Using any Large Language Model(LLM), identify how you can find the orbital period from radius/semi-major axis of the orbit. Make sure to ask follow up questions to make sure you get an equation for orbital period T and radius a (or r). Use 2 different prompts and copy and paste both answers in the 2 cells below. Make sure to include a screenshot of the equation you get.
Prompt 1:
Answer 1:
Prompt 2:
Answer 2:
✅ Question 1.5 (2 points): Which prompt got you the answer with the equation? Why do you think one prompt was better to use than the other?
✎ Do This - Erase the contents of this cell and replace it with your answer to the above question! (double-click on this text to edit this cell, and hit shift+enter to save the text)
The equation that you found is called Kepler’s third law. Using google or any other search engine, try to find the same equation and verify that GenAI gave you the correct answer.
✅ Task 1.6 (1 point): Place a screenshot of the same equation from a reliable source below. Include a reference to that source.
✎ Do This - Erase the contents of this cell and replace it with your answer to the above question! (double-click on this text to edit this cell, and hit shift+enter to save the text)
✅ Question 1.7 (2 points): Using the equation you found in the previous step answer the following question. Planet 1’s orbital radius is 4 times bigger than Planet 2’s orbital radius. They are orbiting the same star. Which planet’s orbital period will be greater? Explain your reasoning.
✎ Do This - Erase the contents of this cell and replace it with your answer to the above question! (double-click on this text to edit this cell, and hit shift+enter to save the text)
Classes#
In Keppler’s third law, there is a constant called the gravitation constant and it has the value \(G = 6.67 \times 10^{-11} \frac{N m^2}{{kg}^2}\). Because this number is constant it means that conceptually its value makes no difference in the effects gravity has. That is why we will set the value of this constant to 1.
✅ Do this 1.8 (2 points): Using the information you found in the previous part, change the class below to calculate the orbital period in the corresponding method of the Planet class.
Make sure to run the cell under the class to make sure your code works correctly. You will get approximately 99.34 as your orbital period if your code is written correctly.
class Planet:
"""
A class representing a planet orbiting a star.
Attributes:
mass (float): The mass of the planet.
orbital_radius (float): The distance of the planet from its star.
star_mass (float): The mass of the star the planet orbits.
"""
def __init__(self, mass, orbital_radius, star_mass):
"""
Initialize a Planet instance with mass, orbital radius, and the mass of its star.
"""
self.mass = mass
self.orbital_radius = orbital_radius
self.star_mass = star_mass
def get_orbital_period(): #add the missing parameters here
"""
Calculate and return the orbital period of the planet.
"""
# here you need to use the equation you found that relates orbital period and radius.
pass
#test your code by running this cell
planet = Planet(2, 100, 4000)
planet.get_orbital_period()
np.float64(99.345882657961)
🛑 STOP#
Pause to commit your changes to your Git repository! (1 points)
Take a moment to save your notebook, commit the changes to your Git repository using the commit message “Committing Part 1”, no need to push the changes to GitHub yet, but you can if you want.
Part 2. Modeling planet migration using Agent Based Modeling (33 points)#
Dimensions#
We are going to try modeling planet interaction with surrounding material using Agent Based Modeling (ABM). For the sake of this assignment, we will keep our model simple. We will assume several things:
All orbits are circular.
Interactions can only change the radius of the orbit, but NOT the shape!
Only forces acting towards the center or outwards from the center radially matter! (The vertical force \(F_r\) in the sketch below)
These assumptions let us look at our system as 2 dimensional BUT only care about radial forces, aka forces acting along the radius of the orbit.
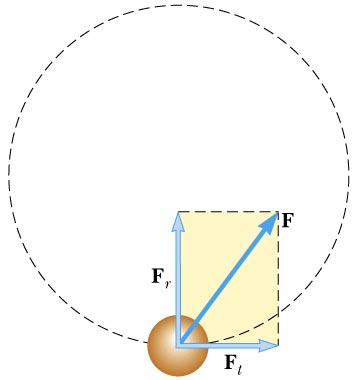
✅ Do this 2.1: (1 points) For the pictures below write down the dimensions of the system.
Picture 1
from IPython.display import Image
# get the image
Image(url="https://raw.githubusercontent.com/sonachitchyan/abm_images/main/system1.png", width=600, height=300)
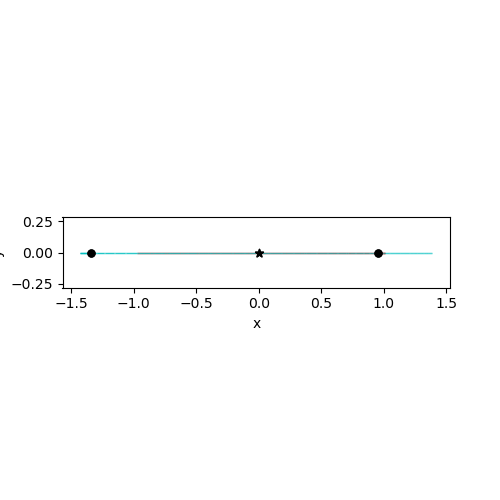
✎ Do This - Erase the contents of this cell and replace it with your answer to the above question! (double-click on this text to edit this cell, and hit shift+enter to save the text)
Picture 2
from IPython.display import Image
# get the image
Image(url="https://raw.githubusercontent.com/sonachitchyan/abm_images/main/system2.png")
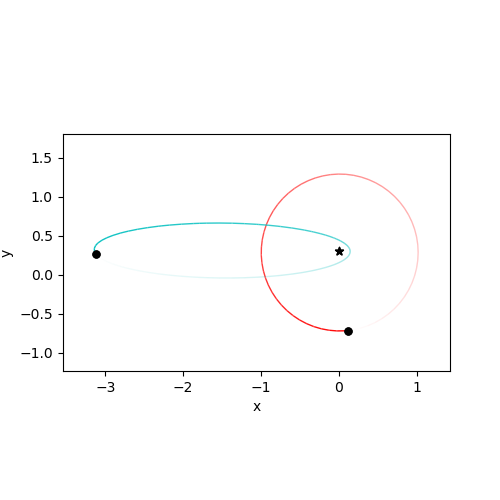
✎ Do This - Erase the contents of this cell and replace it with your answer to the above question! (double-click on this text to edit this cell, and hit shift+enter to save the text)
Model Set-up#
✅ Question 2.2 (1 points): What are the agents of the model in this case?
✎ Do This - Erase the contents of this cell and replace it with your answer to the above question! (double-click on this text to edit this cell, and hit shift+enter to save the text)
✅ Question 2.3 (2 points): How many different classes do we need to model this system? Take into account the agents and the system that we need to run the simulation.
✎ Do This - Erase the contents of this cell and replace it with your answer to the above question! (double-click on this text to edit this cell, and hit shift+enter to save the text)
Modeling a system of 2 planets around a star#
If we have a system of 2 planets orbiting a star, these planets interact with each other gravitationally. This force is proportional to the planets’ masses (bigger mass -> stronger force/interaction) and inversely proportional to the distance between the planets (bigger distance -> weaker force/interaction). If this force is substantial, it can move the planets from their initial orbits, even make them collide in extreme cases! To make sense of how this happens, we can start from a simplified model of 2 planets orbiting the same star. In this part you will create and run that model, plot how the radius from the host star changes for each planet.
✅ Question 2.4 (4 points): Add docstrings to the methods below. You should include a description of what the method does, a description of parameters and and what the method returns.
def calculate_forces(planet1, planet2):
## NOTE: this finds the force planet2 exerts on planet1.
## ADD YOUR DOSCTRING HERE
force_x = planet2.mass * planet1.mass * (planet2.x - planet1.x) / ((planet2.x - planet1.x)**2 + (planet2.y - planet1.y)**2)**(1.5)
force_y = planet2.mass * planet1.mass * (planet2.y - planet1.y) / ((planet2.x - planet1.x)**2 + (planet2.y - planet1.y)**2)**(1.5)
force_radial = force_x * planet1.x/planet1.radius + force_y * planet1.y/planet1.radius
return force_radial
def take_step(planet, force, delta_time):
##NOTE: this function calculates the step that planet takes in delta_t time of the simulation and updates the properties of the planet.
##There is no return because the changes are done to the planet directly.
## ADD YOUR DOSCTRING HERE
acceleration = force / planet.mass
radius_change = 0.5 * acceleration * delta_time**2 + planet.velocity_radial * delta_time
velocity_change = acceleration * delta_time
planet.radius = planet.radius + radius_change
planet.x = planet.radius * np.cos(2 * np.pi * delta_time / planet.orbital_period)
planet.y = planet.radius * np.sin(2 * np.pi * delta_time / planet.orbital_period)
planet.velocity_radial = planet.velocity_radial + velocity_change
if planet.radius < 0.001:
planet.radius = 0
planet.status = "Terminated"
planet.orbital_period = 2 * np.pi * np.sqrt(planet.radius**3/planet.star_mass)
✅ Question 2.5 (3 points): Describe what the code provided above does. What interaction does it describe? Explain both methods separately.
✎ Do This - Erase the contents of this cell and replace it with your answer to the above question! (double-click on this text to edit this cell, and hit shift+enter to save the text)
✅ Question 2.6 (3 points): Turn the following pseudo-code into code:
Class: Planet
- Represents a planet orbiting a star.
Attributes:
- mass (float): Set to the mass of the planet.
- radius (float): Set to the initial orbital radius of the planet.
- star_mass (float): Set to the mass of the star the planet orbits.
- orbital_period (float): Compute using Kepler’s third law:
orbital_period = 2 * pi * sqrt(radius^3 / star_mass).
- velocity_radial (float): Initialize to 0.0.
- x (float): Set to radius (initial x-coordinate of the planet).
- y (float): Set to 0 (initial y-coordinate of the planet).
- status (string): Defaults to "Active". Changes to "Terminated" if the planet falls into the star
(radius < sqrt(0.02)).
Methods:
- __init__:
Assigns the default values to the attributes
Class: System
Represents a planetary system with a central star and two orbiting planets.
Attributes:
- star_mass (float): Set to the mass of the central star.
- planet1 (Planet): Set to the first planet in the system.
- planet2 (Planet): Set to the second planet in the system.
- planet1_pos (list): Initialize as a list of lists with first element [0.0, planet1.radius], tracking planet1's position.
- planet2_pos (list): Initialize as a list of lists with first element [0.0, planet2.radius], tracking planet2's position.
Methods:
- __init__:
Assigns the default values to the attributes.
- evolve(time):
Simulate the evolution of the system over a given time.
- Initialize:
- t (float): Set to 0.0.
- delta_time (float): Set to planet1.orbital_period / 5.
- While t < time:
- Initialize:
- total_force_planet1 (float): Set to 0.0.
- total_force_planet2 (float): Set to 0.0.
- If both planets are "Active" and their squared distance >= 0.02:
- Compute total_force_planet1 using calculate_forces(planet1, planet2).
- Compute total_force_planet2 using calculate_forces(planet2, planet1).
- Update planet1 position using take_step(planet1, total_force_planet1, delta_time).
- Update planet2 position using take_step(planet2, total_force_planet2, delta_time).
- Increment t by delta_time.
- Append [t, planet1.radius] to planet1_pos.
- Append [t, planet2.radius] to planet2_pos.
- If either planet’s status is "Terminated", break the loop.
# your code here
✅ Do this: Explain what the code above does.
✎ Do This - Erase the contents of this cell and replace it with your answer to the above question! (double-click on this text to edit this cell, and hit shift+enter to save the text)
✅ Do this: After defining the System class, complete and run the following cell.
pl1 = Planet(1, 10, 400) # planet with mass 1, radius 10 and star mass 400
pl2 = Planet(1, 20, 400) # planet with mass 1, radius 20 and star mass 400
system = System(400,) # fill in the needed arguments
system.evolve(2000)
Visualization#
✅ Question 2.7 (1 point): Now, taking the saved positions of our planets, we can track how their orbital radius changes with time. To do that, make a scatter plot of orbital radius vs time for both planets using the attributes of the system object. Use different colors and label the lines with “Planet 1” and “Planet 2”. You can use GenAI for this part but don’t forget to add a reference to your answer.
# your code here
✅ Question 2.8 (4 points): Using the plot you made, describe what is happening with the two planets. Is this what you expected to happen?
✎ Do This - Erase the contents of this cell and replace it with your answer to the above question! (double-click on this text to edit this cell, and hit shift+enter to save the text)
Modeling a system of 1 big planet and N small planets around a star#
Now let’s extend our model for a system of 1 big planet (by big we mean Jupiter size planet) and a bunch of small planets around it, which will be an approximation for the disk.
Here we will provide the generalized code that runs for a set number of planets.
class System:
def __init__(self, star_mass, planet_list):
# the primaty planet we care about is the first planet in the list
self.star_mass = star_mass
self.planet_list = planet_list
self.number_of_planets = len(planet_list)
self.plot_positions = [[0.0, planet_list[0].radius]]
def evolve(self, time):
t = 0.0
delta_time = self.planet_list[0].orbital_period/5
while t < time:
# delta_t = self.planet_list[0].orbital_period/5 ## this is the step that chooses the resolution of our simulation
total_force_list = np.zeros(self.number_of_planets)
for i, planet in enumerate(self.planet_list):
if planet.status == "Active":
total_force_radial = 0.0
for other_planet in self.planet_list:
if other_planet.status == "Active":
if other_planet != planet and (other_planet.x - planet.x)**2 + (other_planet.y - planet.y)**2 >= 0.02:
total_force_radial += calculate_forces(planet, other_planet)
total_force_list[i] = total_force_radial
for i, planet in enumerate(self.planet_list):
if planet.status == "Active":
take_step(planet, total_force_list[i], delta_time)
for planet in self.planet_list:
if planet.radius < 0.02:
planet.status == "Terminated"
if self.planet_list[0].status == "Terminated":
break
t += delta_time
self.plot_positions.append([t, self.planet_list[0].radius])
✅ Question 2.9 (4 points): How is the code above different from what you wrote for a 2 planet system?
✎ Do This - Erase the contents of this cell and replace it with your answer to the above question! (double-click on this text to edit this cell, and hit shift+enter to save the text)
✅ Question 2.10 (3 points): Run a simulation for a system of 51 planets orbiting a star with mass 400. The first planet of the list is the primary planet with mass 150 at radius 1, and the rest of the planets each have a mass of 0.1 and are evenly placed between 0.01 and 0.7 radii. Run the simulation for time of 10.
#your code here
Visualization#
✅ Question 2.11 (1 point): Make the same visualization for radius vs time for the big planet. You can use GenAI for this part but don’t forget to add a reference to your answer.
#your code here
✅ Question 2.12 (2 points): Describe what is happening to the planets’ orbits based on the plot you made.
✎ Do This - Erase the contents of this cell and replace it with your answer to the above question! (double-click on this text to edit this cell, and hit shift+enter to save the text)
✅ Question 2.13 (4 points): Was this what you expected to see based on the concept of planetary migration? Explain why.
✎ Do This - Erase the contents of this cell and replace it with your answer to the above question! (double-click on this text to edit this cell, and hit shift+enter to save the text)
🛑 STOP#
Pause to commit your changes to your Git repository! (1 points)
Take a moment to save your notebook, commit the changes to your Git repository using the commit message “Committing Part 2”, no need to push the changes to GitHub yet, but you can if you want.
If you like, you can upload this file to D2L for a record. Nevertheless, we will grade the copy on GitHub.
Post-assignment Survey#
Please fill out the post-assignment survey here.
© Copyright 2024, Department of Computational Mathematics, Science and Engineering at Michigan State University
